

Therefore, when distances are reciprocally proportional to weights, the moments are equal, as Archimedes demonstrated in The Book on Equal Moments. Therefore, a body acquires weight from both quantity and quality, but a weight receives its moment from the distance at which it is suspended. Therefore, there exists a certain third kind of power or third difference of magnitude-one that differs from both body and weight-and this they call moment.

For a weight suspended at a greater distance is heavier, as is obvious in a balance. " equal weights at unequal distances do not weigh equally, but unequal weights weigh equally. Here is a Latin to English translation as given by Marshall Clagett: In 1554, Francesco Maurolico clarifies the Latin term momentum in the work Prologi sive sermones. That said, why was the word momentum chosen for the translation? One clue, according to Treccani, is that momento in Medieval Italy, the place the early translators lived, in a transferred sense meant both a "moment of time" and a "moment of weight" (a small amount of weight that turns the scale). The same term is kept in a 1501 translation by Giorgio Valla, and subsequently by Francesco Maurolico, Federico Commandino, Guidobaldo del Monte, Adriaan van Roomen, Florence Rivault, Francesco Buonamici, Marin Mersenne, and Galileo Galilei. Īround 1450, Jacobus Cremonensis translates ῥοπή in similar texts into the Latin term momentum ( lit.

The term ῥοπή is transliterated into ropen. In 1269, William of Moerbeke translates various works of Archimedes and Eutocious into Latin. Moreover, in extant texts such as The Method of Mechanical Theorems, moments are used to infer the center of gravity, area, and volume of geometric figures. In particular, in extant works attributed to Archimedes, the moment is pointed out in phrasings like: The context of these works is mechanics and geometry involving the lever. "inclination") and composites like ἰσόρροπα ( isorropa, lit. In works believed to stem from Ancient Greece, the concept of a moment is alluded to by the word ῥοπή ( rhopḗ, lit. This technique applies to small objects such as molecules, īut has also been applied to the universe itself, being for example the technique employed by the WMAP and Planck experiments to analyze the cosmic microwave background radiation. Measurements pertaining to multipole moments may be taken and used to infer properties of the underlying distribution. (such as force or electrical charge) at that point: In its most basic form, a moment is the product of the distance to a point, raised to a power, and a physical quantity Commonly used quantities include forces, masses, and electric charge distributions.
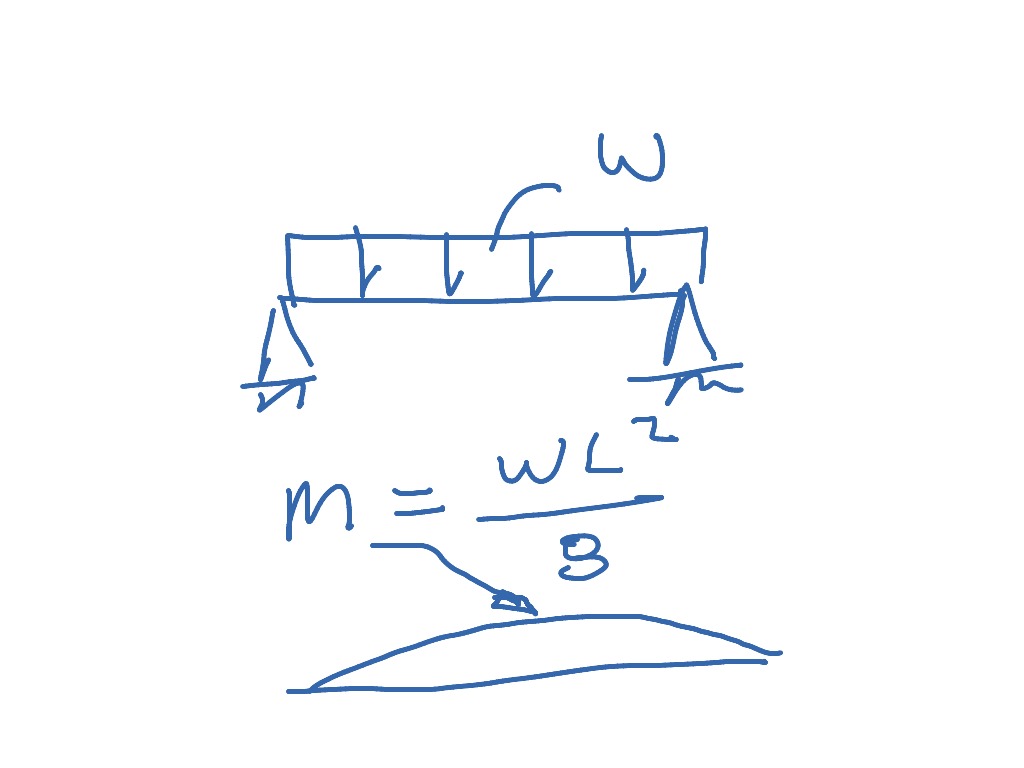
In principle, any physical quantity can be multiplied by a distance to produce a moment. For example, the moment of force, often called torque, is the product of a force on an object and the distance from the reference point to the object. In this way, the moment accounts for the quantity's location or arrangement. Moments are usually defined with respect to a fixed reference point and refer to physical quantities located some distance from the reference point. In physics, a moment is a mathematical expression involving the product of a distance and physical quantity.


 0 kommentar(er)
0 kommentar(er)
